The Monty Hall problem modeled in Python
You've all heard this classic statistics problem, based on an old game show:
A contestant is shown 3 doors. Only one of those three doors hides something of value to the contestant (perhaps a new car), while the other two contain nothing. The contestant chooses one door, but that door remains closed. The host then opens up a 2nd door, and this door is always a losing door. At this point, the contestant may choose to now open the originally-chosen door, or switch to and open the last remaining door.
So why is this interesting? It turns out that the way to maximize your chances of winning is to always switch, and this maximized chance is 67%. It also turns out that this is totally non-intuitive and that most people think that the chances of winning are at best 50% whether you switch or not.
If you haven't heard the solution to this problem before, you should think through it and see what you expect the chances of winning are under the two conditions: After the contestant chooses a door, and is subsequently shown that one of the other two is a losing door, [1] the contestant always switches to the remaining door, or [2] the contestant never switches.
Whether the contestant is always or never switching, the outcomes only rely on the initial choice (see Figures 1 & 2 below). The easy case is when the contestant does not switch. Since only 1 of the 3 doors is a winning door, the contestant will only choose that door 1/3 of the time, meaning that they will only win 1/3 (33%) of the time.
When the contestant always switches after the host's reveal of a losing door, the outcome is still decided by the initial choice. Say the contestant chooses the only winning door (Fig.1). This happens 1/3 of the time. In that case, a switch will always be to a losing door. So, we already know that the contestant loses at least 1/3 of the time.
Now what happens when the contestant chooses a losing door (Fig. 2)? This happens 2 out of 3 times. In that case, what remains will be the single winning door and the other losing door. However, the host always opens a losing door. Therefore, the host will show the contestant the only other losing door, and then only the winning door remains. If the contestant switches, they can only switch to the winning door.
So, when the contestant always switches, they will win every time the initial choice was wrong (2/3 of the time), and lose every time the initial door was correct.
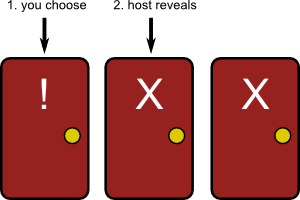
Fig.1: By chance, your first choice will be correct 1/3 of the time. If you always switch, you will always be wrong in this case.
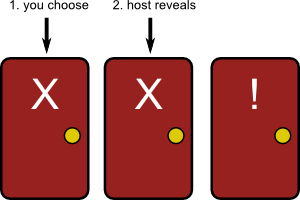
Fig.2: By chance, your first choice will be incorrect 2/3 of the time. The host then reveals the only remaining false door, so that only the winning door is left. If you always switch, you will always be correct in this case.
Hopefully that makes intuitive sense. Now here's the fun part. Say you wanted to expand this problem: given D doors, W of which are winning doors, how does the probability of winning change when choosing to always or never switch? We can model any case described in this way in Python:
import random
class Monty:
""" A class representing an in instance of the Monty Hall problem."""
def __init__( self, true_doors, total_doors ):
""" Initialize a Monty object, given the winning and total doors.
Inputs:
true_doors - an integer representing the number of "winning" doors
total_doors - an integer representing the total number of doors
Obviously, total_doors must be greater than true_doors
"""
self.true_doors = true_doors
self.total_doors = total_doors
# Set up a dictionary of i:False pairs, with each i representing one
# of the total doors. Doors can then be chosen by an integer key
self.doors = { i:False for i in range( total_doors )}
self.set_true_doors()
def set_true_doors( self ):
""" Randomly choose self.true_doors keys in self.doors, setting value to True."""
for win in range( self.true_doors ):
potential_winner = self.random_door()
# The randomly-chosen door may already be set to true, in the
# case where self.true_doors is > 1. There must be EXACTLY
# self.true_doors values set to True:
while self.doors[ potential_winner ]:
potential_winner = self.random_door()
self.doors[ potential_winner ] = True
def choose_random_door( self ):
""" Choose a random door, and set the value of self.win to its value."""
self.choice = self.random_door()
self.win = self.doors[ self.choice ]
def switch_choice( self ):
""" Make one False door off-limits, and switch the chosen door to another."""
revealed = self.reveal_false_door()
new_choice = self.random_door()
while new_choice == self.choice or new_choice == revealed:
new_choice = self.random_door()
self.choice = new_choice
self.win = self.doors[ self.choice ]
def reveal_false_door( self ):
""" Randomly choose a self.door key whose value is False."""
false_door = self.random_door()
while self.doors[ false_door ] or self.choice == false_door:
false_door = self.random_door()
return false_door
def random_door( self ):
""" Return a random value between 0 and (self.total_doors-1)."""
return random.randint( 0, self.total_doors-1 )
def main():
total = int(input( 'Total number of doors: '))
trues = int(input( 'Number of winning doors: '))
trials= int(input( 'Number of trials: '))
if input( 'Switch after reveal?: ').upper()[0]=='Y':
switch = True
else: switch = False
wins = 0
for n in range( trials ):
monty_hall = Monty( trues, total )
monty_hall.choose_random_door( )
if switch: monty_hall.switch_choice( )
if monty_hall.win: wins += 1
print( 'Percent win:', wins/trials ); input()
if __name__ == '__main__':
main()
Run this with any scenario you like!